Sobre los números imaginarios

El cuadrado de un número es positivo, incluso cuando el original es negativo. Entonces, ¿cuál es la solución de una ecuación del tipo x^2=-1 si tanto 1 como -1 al cuadrado dan uno?

Pero para hablar de números imaginarios, antes deberíamos hablar del resto. Hablamos de conjuntos numéricos, y es que hasta los números han evolucionado conforme lo hemos hecho nosotros.

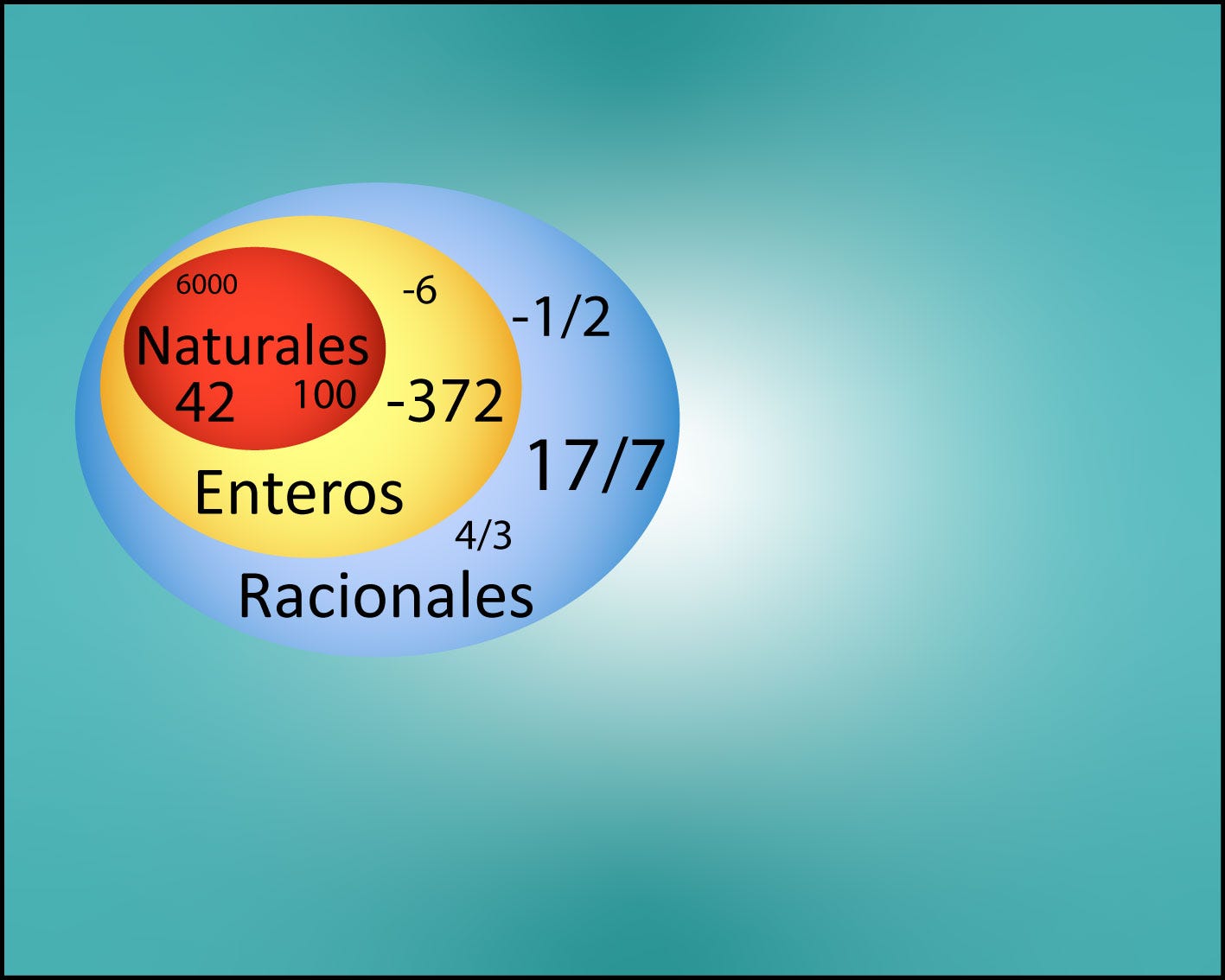
El conjunto más básico es el de los naturales, es decir, los que usamos para contar por ejemplo cuántas manzanas tenemos. ¿El cero entraría en esta definición? Es una pregunta interesante, por desgracia Twitter solo acepta 280 caracteres por tuit, no nos cabe la respuesta.

Es evidente que esta clasificación está muy incompleta, puesto que solo tiene en cuenta números positivos. ¿Qué ocurre con x + 3 = 1? Necesitamos una categoría mayor, la de los enteros, que engloba positivos y negativos, desde el menos infinito hasta el infinito.

Esta vez sí, el cero está incluido, seguro. Pero ¿y los no enteros? ¿Qué hay de por ejemplo 2*x = 3? Necesitamos una categoría aún mayor, los llamados racionales, que recogería a todos los números que podemos expresar como una fracción. Además de a todos los anteriores.

En esta categoría no afecta si es un número finito, como 1/2 = 0,5, o uno infinito, como 2/3 = 0,666… Lo importante es que seamos capaces de saber cuáles son sus cifras. Incluso aunque sea un número en el que cueste encontrar su periodicidad como 17/7 = 2,428571428571…

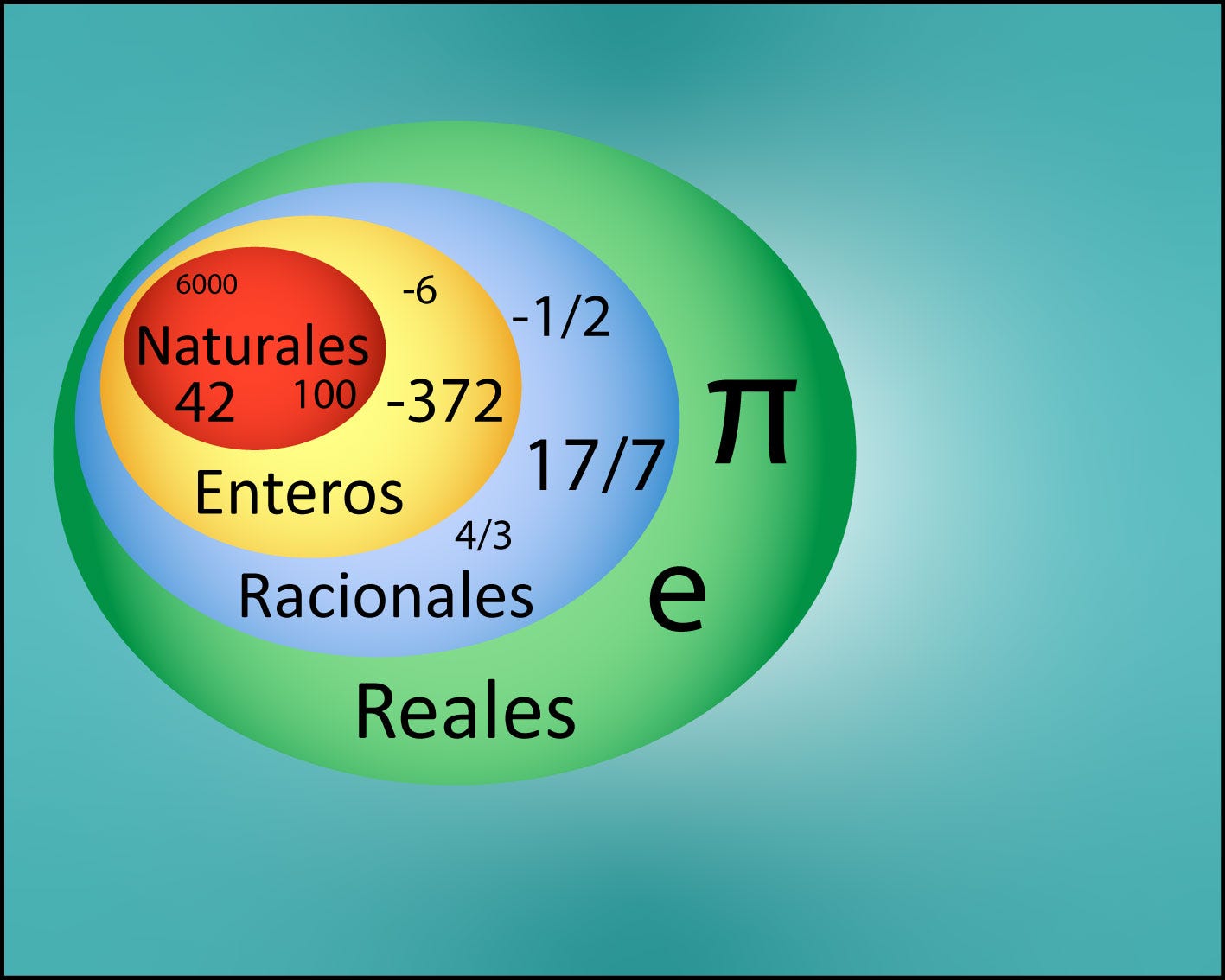
El conjunto de los racionales parece bastante completo, pero aún quedan números no enteros imposibles de expresar así. Un ejemplo claro lo tenemos si intentamos averiguar pi. No solo es un número infinito, sino que sus cifras no se repiten por mucho que busquemos.

A este tipo de números irracionales los llamamos reales, el número pi o el número de Euler son buen ejemplo de sus características. Con eso podría parecer que hemos terminado, que hemos incluido a todos los números por raros que sean.

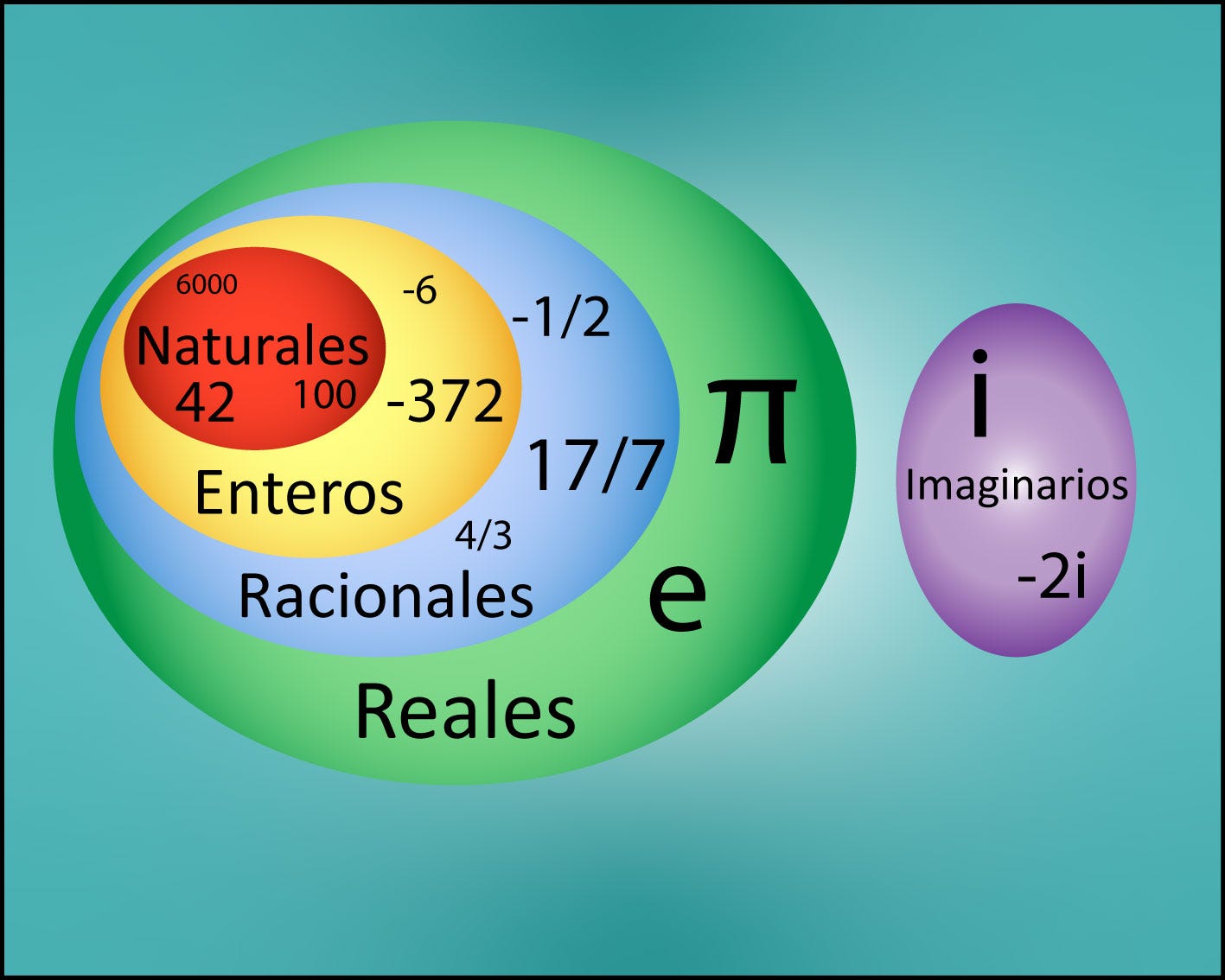
Pero es entonces cuando recordamos la expresión de la discordia original x^2=-1. La raíz cuadrada de un número negativo. ¿Qué hacemos con esto?

Cualquier número que multiplique por él mismo dará como resultado un número positivo. Porque, aunque ese número sea negativo, un número negativo multiplicado por otro negativo da siempre positivo.

No hay ningún número dentro de los reales que multiplicado por sí mismo dé -1, es necesario definir otra clase. La solución a dicha ecuación es raíz de menos uno, a lo que se suele denominar como i. Como puede verse i^2 = -1. Esto es lo que llamamos un número imaginario.

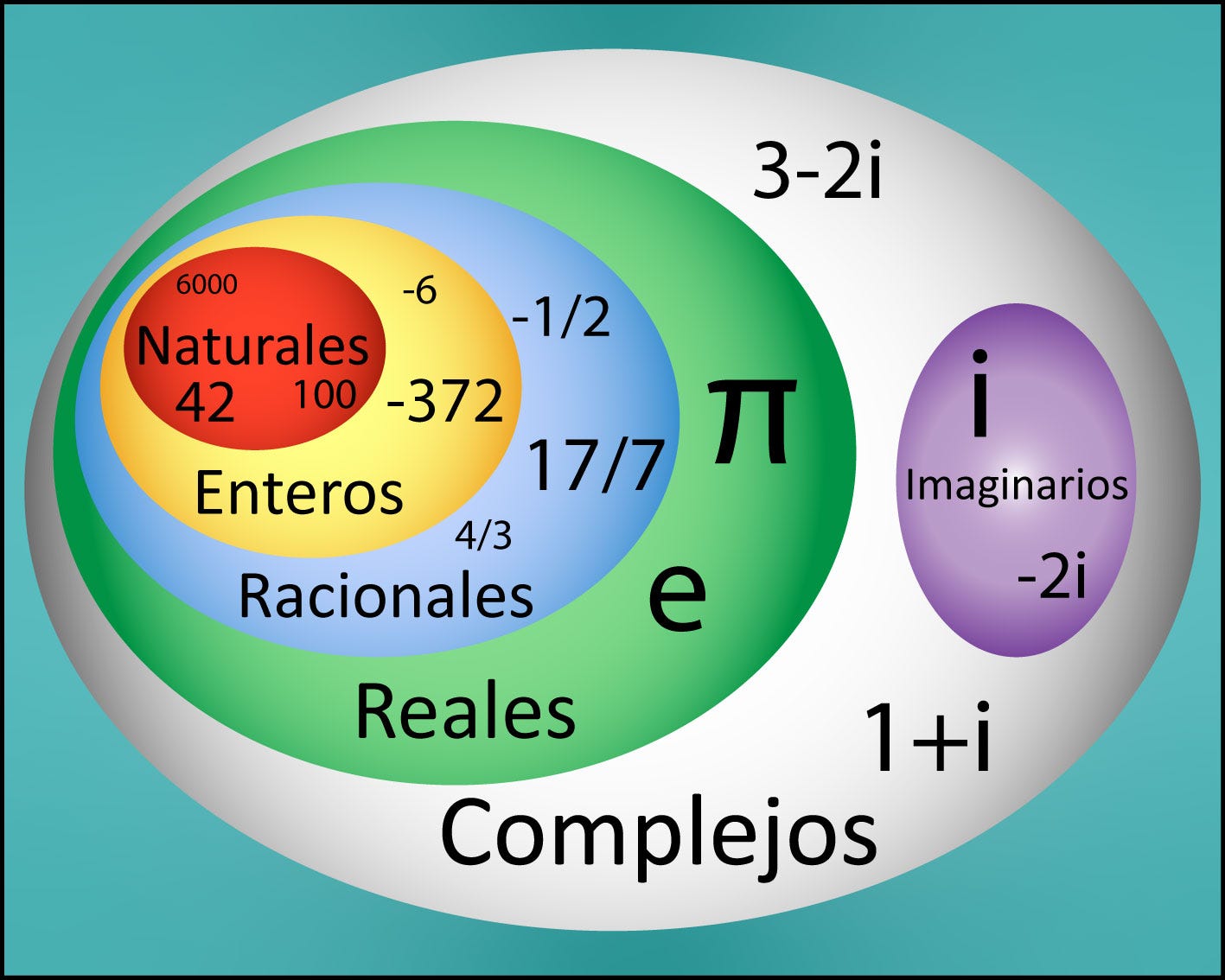
Si además tenemos un número con parte real, como podría ser 3 + 2*i, por ejemplo, lo que tenemos en un número complejo. Con lo que todos los números reales serían números complejos con una parte imaginaria nula.

Esto nos permite enunciar el teorema fundamental del álgebra según el cual cualquier polinomio de grado mayor que cero, grado n, tendrá siempre n raíces dentro del conjunto de los números complejos.

Estos números complejos, con su parte real e imaginaria, surgen constantemente en física. Puede que a estos números se les llame imaginarios, pero la física que describen es muy real.