Radiación de Hawking y evaporación de agujeros negros.

Hawking, después de aseverar que era algo imposible, dio una prueba de que los agujeros negros emiten radiación y encima “se evaporan”. ¿Cómo?

May 02, 2023

Supongamos que estás en una nave orbitando a un agujero negro (AN). Estás disfrutando de una de las vistas más privilegiadas del universo y decides hacerte un café. Pero en lugar de azúcar le echas sal, así que lo tiras al agujero negro ¿Qué otra cosa podrías hacer?

Texto: “Por sus características hay 4 tipos de agujeros negros.” En cuatro columnas esquema de las posibles configuraciones. De izquierda a derecha: en la primera pone “Schwarschild” y aparece un círculo con una m de masa dentro, debajo pone “sin rotación ni carga”. En la segunda pone “Kerr” y aparece un círculo con una m dentro y una flecha para señalizar su rotación, debajo pone “en rotación sin carga”. En la tercera pone “Reissmer-Nordström y aparece un círculo con una m y una q (de carga) debajo pone “sin rotación con carga”. En la cuarta y última pone “Kerr-Newman” y aparece un círculo con una m y una q con una flecha para señalizar que está rotando, debajo pone “con carga con rotación”. Texto: “Los agujeros negros solo tienen masa, momento angular (rotación) y carga.”

Mientras observas como el agujero negro hace desaparecer tu error, te paras a pensar. Si, por el teorema de unicidad o de no pelo, un AN solo se caracteriza por su masa, momento angular y carga, ¿habría alguna diferencia si le hubieses puesto azúcar antes de arrojarlo?

Texto: “Esta pregunta nos llevará a hablar de: - Entropía de los agujeros negros (junto con su fórmula que se explicará más adelante) - Termodinámica de los agujeros negros (junto con la fórmula de la temperatura que se explicará más adelante). - Conceptos previos para hablar de la radiación de Hawking. - Radiación de Hawking. - Evaporación de agujeros negros.”

¿Habría alguna diferencia si se hubiera quedado frío? En un principio serían sistemas con diferente entropía, pero una vez dentro del agujero negro todo sería lo mismo. ¿Es eso posible? ¿Desaparece la entropía? Este supuesto sería una violación de la 2ª ley de la termodinámica.

Felpudo con el mensaje: "En esta casa se respetan las leyes de la termodinámica".

Una pregunta similar le planteó John Wheeler en 1971 a su doctorando, Jacob Bekenstein, según explica Bekenstein en su artículo "The Limits of Information" (https://arxiv.org/abs/gr-qc/0009019).

Bekenstein se fundamentó en que la solución tenía que estar en las propiedades del propio agujero negro y no en las de lo que arrojas. Los agujeros negros deben tener entropía y tiene que poder determinarse a partir de lo que se observa de él.

El punto de partida es que la entropía tiende a aumentar. Una posibilidad era que tuviera relación directa con la masa del AN. Aunque esto presentaba un problema y es que sabían que en una colisión de ANs se pierde masa en forma de radiación gravitatoria, y con ella entropía.

La masa no parecía ser la respuesta, pero ese mismo año Hawking demostró que el área del horizonte de sucesos de un agujero negro siempre aumenta. Bekenstein concluyó que ahí tenía que estar la respuesta. La entropía de un agujero negro debe ser proporcional a su área.

Bekenstein pudo deducir la expresión que debía de describir esta entropía exceptuando el factor ¼ que fue calculado por Hawking años después. Dando así la entropía de Bekenstein-Hawking para los agujeros negros.

Fórmula de la entropía de Bekenstein-Hawking: la constante de Boltzmann por la velocidad de la luz al cubo por su área dividido entre (4 por la constante de Planck y la constante de gravitación universal). La constante de Planck es 1,055 por diez elevado a menos 34 J*S, la de gravitación universal es 6,67 por diez elevado a menos 11 Nm^2/Kg y la de Boltzmann 1,38 por diez elevado a menos veinte-tres J/K El 4 de la parte de abajo de la fracción fue calculado por Hawking.

Había resuelto el problema propuesto por Wheeler. La suma de la entropía del agujero negro y la del exterior siempre aumenta. A esto se le conoce como segunda ley de la termodinámica generalizada (SGL).

Dibujo en el que aparece un círculo que representa un agujero negro con “incremento de entropía del agujero negro” escrito dentro. Fuera del círculo aparece el “incremento de entropía del exterior”. Aparece escrito que “el incremento de la entropía total será el incremento de la entropía del agujero negro más el incremento de la entropía del resto del universo”. Esto es la segunda ley de la termodinámica generalizada.

De hecho, la entropía en un agujero negro es enorme. Para hacernos una idea, la entropía de un AN de la masa del Sol es más de 20 órdenes de magnitud superior que la de una estrella con la misma masa. Lo cual tiene bastante sentido.

Dibujo sencillo en el que aparecen dos círculos, el de la izquierda representa a una estrella como el sol, cuya entropía es del orden de diez elevado a cincuenta y siete. El de la derecha representa un agujero negro de la misma masa cuya entropía es del orden de diez elevado a setenta y nueve. En el segundo caso es 22 órdenes de magnitud superior, “la entropía de un agujero negro es enorme”.

Como hemos dicho, un agujero negro se caracteriza por su masa, momento angular y carga. Por tanto, la cantidad de microestados compatibles con el estado final en el que se encuentra es enorme.

Resolvió el problema, pero surgió otro. Su conclusión sugiere una relación entre la física de los agujeros negros y la termodinámica, como explicó en su artículo "Black holes and entropy" en el año 1973 (https://journals.aps.org/prd/abstract/10.1103/PhysRevD.7.2333).

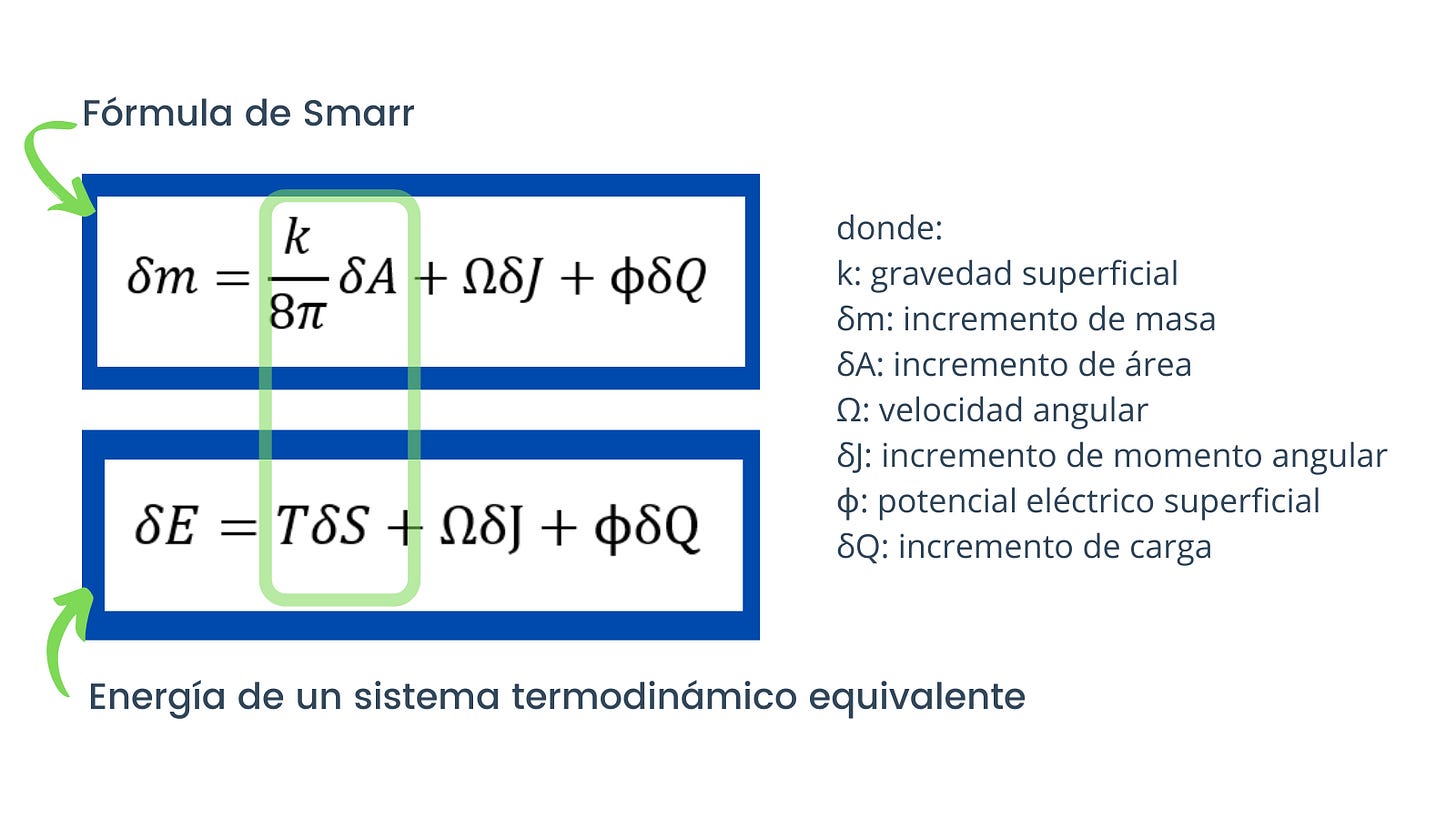
Una de las cosas que le hizo ver esta relación fue la similitud entre la ecuación para expresar la variación de masa de un agujero negro en función de su área, momento angular y carga (ecuación de Smarr) con la energía de un sistema cargado en rotación.

Fórmula de Smarr: cambio de masa igual a la gravedad superficial entre 8pi por el incremento de área más la velocidad de rotación por el cambio de momento angular más potencial eléctrico superficial por el cambio de carga. Energía de un sistema termodinámico equivalente: cambio de energía igual a la temperatura por el cambio de entropía más la velocidad angular por de cambio en el momento angular más el potencial eléctrico superficial por el cambio de carga. La comparación entre ambas formulas destaca la relación de la temperatura con la gravedad superficial del agujero negro.

Si asemejamos el agujero negro a un sistema termodinámico en rotación y cargado, comparando la expresión de su energía con la ecuación de Smarr y teniendo en cuenta la relación entre la masa y la energía, podemos apreciar esta relación.

Puede verse que acompañada de la entropía (o el área) tenemos una temperatura. La temperatura de un agujero negro. Significase eso lo que sea que quisiera significar. Esta es la expresión a la que se pudo llegar para la temperatura de un AN. Que, por cierto, es muy pequeña.

Texto: “Caso del agujero negro de Schwarschild” Fórmula: La temperatura del agujero negro será igual a la constante de Planck por la velocidad de la luz al cubo dividido entre (8*pi, la constante de gravitación universal, la constante de Boltzmann y la masa del agujero negro). Texto: “Donde: La constante de Planck es 1,055 por diez elevado a menos 34 J*S, la de gravitación universal es 6,67 por diez elevado a menos 11 Nm^2/Kg y la de Boltzmann 1,38 por diez elevado a menos veinte-tres J/K”.

Por lo que hemos podido ver, la temperatura de los agujeros negros y su termodinámica ya aparece desarrollada en la tesis de Bekenstein en el año 1972 (Baryon number, entropy, and black hole physics). Aunque por desgracia no hemos podido encontrar la tesis completa.

Recorte del índice de la tesis de la Bekenstein, en concreto del capítulo diez donde aparece la termodinámica de los agujeros negros.

Sin embargo, esta idea de la termodinámica de los agujeros negros no fue ampliamente aceptada, por decirlo de forma amable. El pensamiento de que un agujero negro pudiera tener temperatura chocaba demasiado con lo establecido hasta el momento.

En el mejor de los casos podían aceptar la relación matemática entre el área con la entropía y la gravedad superficial con la temperatura.

No es de extrañar. Asumir que un agujero negro tiene temperatura implicaría que está emitiendo algo, y sabían (o creían saber) que nada escapa de un agujero negro. Curiosamente, una de las voces más críticas con las ideas de Bekenstein fue Stephen Hawking.

Una muestra de esto se vio cuando Hawking, Bardeen y Carter publicaron en 1973 su artículo "The four laws of black holes mechanics" para tratar de dar una explicación mecánica en lugar de una termodinámica. (https://link.springer.com/article/10.1007/BF01645742)

En este artículo (firmado por Hawking) se deja claro que la temperatura de un agujero negro debe ser cero, puesto que no puede emitir nada. Otro punto divertido de esto es que, según el propio Bekenstein, este artículo se referencia mucho al tratar la termodinámica de los ANs.

Este artículo aparece como recibido el 24 de enero de 1973. Pero en septiembre de ese mismo año Hawking viajó a Moscú donde Yakov B. Zel´dovich y su doctorando Starobinsky le mostraron que, teniendo en cuenta los efectos cuánticos, un agujero negro en rotación emite partículas.

Su argumento se basaba en el hecho de que una esfera metálica en rotación emite radiación electromagnética. Por tanto, por analogía, un agujero negro en rotación también lo haría. A esto se le conoce como superradiancia. Una idea que le dio mucho en que pensar a Hawking.

La forma que tenemos de describir los agujeros negros es la relatividad general, según la cual nada escapa de un AN. Aquí no hay sorpresas. Pero también sabemos que carecemos de una teoría cuántica de la gravedad, con lo cual los efectos cuánticos no están tenidos en cuenta.

A Hawking le interesó la hipótesis de Zel´dovich, aunque no sus métodos. Así que los replanteó. Para ello, y a falta de una teoría cuántica de la gravedad, utilizó la teoría cuántica de campos en espacio-tiempo curvo.

Una unión forzosa de la relatividad general con la teoría cuántica de campos en la que la primera se encarga del espacio-tiempo y la segunda de los efectos cuánticos. Esta aproximación a una teoría cuántica de la gravedad funciona porque se trabaja lejos de la singularidad.

Con esta herramienta llegó a una conclusión que sorprendió al mundo entero. Sí, los agujeros negros en rotación emiten partículas... Y los que no rotan también. Este resultado fue publicado en su artículo "Black hole explosions?" (https://www.nature.com/articles/248030a0).

Esa primera publicación fue de 1974, pero una explicación mucho más detallada la dio en su artículo "Particle Creation by Black Holes" en 1975. Expliquemos como llegó hasta este resultado. (https://www.worldscientific.com/doi/abs/10.1142/9789814539395_0011)

En este punto es común ver una explicación tal que: un par de partículas se generan por un instante, pero antes de poder aniquilarse una cae al agujero negro y la otra escapa. Generando así la radiación de Hawking.

El propio Hawking da esta idea en su artículo de 1975... Para después añadir que es una imagen demasiado heurística y que no debe ser tomada en serio.

La explicación anterior, aunque problemática, es útil para hacerse una idea del concepto. Aun así, tenemos la ilusión de tratar de explicar la lógica que siguió Hawking para llegar a este resultado. Eso requiere un poco de teoría cuántica de campos.

Estudiando el tema, creemos que podemos explicar esta lógica si introducimos dos conceptos previos: el oscilador armónico y el campo de Klein-Gordon. Vamos a ello.

1. Texto: “¿Qué necesitamos del oscilador amónico cuántico?” Aparece el hamiltoniano expresado en función de su momento y energía potencial para ser expresado después en términos de los operadores escalera (esto se explicará después). Se destaca que lo que necesitamos recordar es la forma del hamiltoniano (que explicaremos más adelante) y el concepto de los operadores escalera. También hay un pequeño esquema con los diferentes estados cuánticos posibles siendo este una especie de U con líneas paralelas a lo largo de ella. En este sistema el operador a disminuye un nivel de energía y el operador a daga lo sube.

2. Texto: “¿Qué necesitamos del campo de Klein-Gordon?” Aparece su hamiltoniano completo y después el mismo siendo reexpresado en términos de los operadores creación y destrucción que serán equivalentes a los operadores escalera del oscilador armónico. Esto será posible por la similitud entre ambos hamiltonianos. Se define el vacío como el estado donde el operador destrucción sobre ese espacio siempre sea nulo. Esto se desarrollará más adelante.

El oscilador armónico cuántico es el análogo al oscilador clásico. Es decir, un sistema que cuando se deja en libertad lejos de su punto de equilibrio describe oscilaciones alrededor de este. El péndulo sería un ejemplo de esto.

Una de las diferencias entre el oscilador cuántico y el clásico es que en mecánica cuántica los niveles energéticos a los que puede acceder están cuantizados, o lo que es lo mismo, son discretos en lugar de continuos. Aquí aparece el hamiltoniano.

En mecánica cuántica el hamiltoniano será el operador que represente la energía total del oscilador y nos permitirá calcular cuales son los niveles de energía posibles. Para este caso del oscilador armónico cuántico, el hamiltoniano vendrá dado por la siguiente expresión.

A la izquierda de la imagen aparece el potencial en forma de pozo, se asemeja a una U con líneas paralelas en ella que representan los diferentes niveles energéticos posibles. A la derecha aparece el hamiltoniano del oscilador armónico. Se especifica que los posibles niveles para la energía están cuantiados (son discretos).

Necesitamos obtener los niveles de energía posibles para este sistema. La forma más simple de hacerlo es utilizar el método de los operadores escalera, desarrollado por Dirac.

Para ello aplicamos el siguiente cambio de variables en función de estos operadores, a y a daga. Estos serán, respectivamente, los operadores escalera de bajada y de subida.

Cambio que es necesario realizar para poder expresar el hamiltoniano en términos de los operadores escalera.

Este resultado nos permite reescribir el hamiltoniano en función de estos operadores. Además de ver de forma inmediata los valores propios del hamiltoniano o, lo que es lo mismo, los posibles niveles energéticos.

A la izquierda el hamiltoniano en términos de los operadores escalera. Que será H = W(a daga*a + ½). A la derecha (unidos por una flecha verde) Tenemos la ecuación que nos dará la energía de los diferentes niveles energéticos que será E = W(n + ½). Abajo pone que el operador a daga aumenta un nivel energético y el a lo disminuye.

El resultado será que el operador a hará que el sistema disminuya a un nivel inferior de energía. Mientras, el operador a daga tendrá el efecto contrario produciendo que el sistema suba en un nivel de energía.

Diferentes ejemplos de la aplicación de estos operadores en dos filas. En la de arriba se ejemplifica el de subida con los siguientes tres ejemplos: |1> = a daga |0>, |2> = a daga |1>, |n> = (a daga)^n |0>. En la fila de abajo se ejemplifica el de bajada con los siguientes dos ejemplos: |0> = a|1> y |1> = a|2>.

Esta explicación no nos valdría para aprobar un examen de mecánica cuántica, pero esperamos que nos sirva para introducir los dos conceptos que necesitamos: la forma del hamiltoniano de un oscilador armónico cuántico y los operadores escalera.

“¿Qué necesitamos del oscilador amónico cuántico?” Aparece el hamiltoniano expresado en función de su momento y energía potencial para ser expresado después en términos de los operadores escalera (esto se explicará después). Se destaca que lo que necesitamos recordar es la forma del hamiltoniano (que explicaremos más adelante) y el concepto de los operadores escalera. También hay un pequeño esquema con los diferentes estados cuánticos posibles siendo este una especie de U con líneas paralelas a lo largo de ella. En este sistema el operador a disminuye un nivel de energía y el operador a daga lo sube.

Pasemos al campo de Klein-Gordon y a la teoría cuántica de campos. Este tema surgió cuando se intentó entender procesos que suceden a escalas muy pequeñas, donde la mecánica cuántica es relevante, a velocidades muy altas, donde los efectos relativistas también son importantes.

Se encontraron con toda serie de problemas: que las ecuaciones para describir funciones de onda de partículas a velocidades relativistas den pie a soluciones de energía negativa, problemas de causalidad al poder moverse incluso más rápido que la luz…

Uno de los intentos de lograr una ecuación para la función de onda de una partícula relativista fue la de Klein-Gordon. Aunque no era compatible con la mecánica cuántica, a pesar de serlo con la relatividad especial.

Ecuación de Klein-Gordon. La derivada segunda del campo más la masa al cuadro igual a cero.

Como hemos dicho antes, las ecuaciones no funcionaban como se esperaba al trabajar con funciones de onda, aun así esta nos viene genial para describir un campo escalar libre. Pues es lo que necesitamos para poder abordar el trabajo de Hawking.

El hamiltoniano de este campo es este y muy pronto vamos a ver que, aunque no lo parezca a simple vista, es muy parecido al del oscilador armónico.

Hamiltoniano del campo de Klein-Gordon. Es una integral en todo el espacio en tres dimensiones. En este momento muy diferente al obtenido para el oscilador armónico cuántico.

Haciendo el siguiente cambio en el hamiltoniano podemos volver a expresarlo en función de los operadores escalera. Así se evidencia su similitud con el caso del oscilador y nos permite interpretar este campo como una colección de infinitos osciladores armónicos no acoplados.

Cambio realizado para llegar hasta el siguiente hamiltoniano: H = a la integral del momento en las tres dimensiones de 1/(2*pi)^3 * W sub p(a daga * a + ½ del conmutador entre a y a daga). Al comparar este resultado con el del oscilador armónico cuántico su similitud es evidente. Esto nos permite ver este campo como una unión de infinitos osciladores armónicos cuánticos desacoplados.

Eso sí, ahora los operadores escalera tienen otra interpretación, en esta solución representan los operadores de creación y destrucción. Estas excitaciones del campo son las que generan y destruyen partículas.

Formulación de lo expresado en el tuit. Hay dos filas, en la de arriba aparece a daga|0> “Crea” una partícula con momento p. En la de abajo aparare a|1> = |0> “Destruye una partícula con momento p.

Hemos tenido que dar un rodeo, pero necesitábamos esto para poder definir el estado cuántico de vacío. El vacío será el estado sobre el cual la aplicación del operador destrucción para cualquier momento siempre da cero. Un estado en el que no hay ninguna partícula.

(a sub p) |0> = 0 para cualquier p. Esta es la definición de vacío.

Ahora sí, después de abusar de vuestra paciencia, volvamos al trabajo de Hawking.

Su punto de partida fue una estrella colapsando en un agujero negro. Este escenario da un espacio dividido en tres partes: la zona del agujero negro formándose con su espacio-tiempo curvado y las zonas antes y después de él con un espacio-tiempo plano.

En esta situación estudió el comportamiento de un campo escalar sin masa, descrito por la ecuación de Klein-Gordon, porque era un caso sencillo. Asumió que en la primera zona estamos en el vacío. Es decir, el operador destrucción sobre él siempre es nulo.

Resulta que cuando analizamos este mismo campo en la zona cercana al agujero negro esta situación se vuelve un poco más interesante. A partir de las soluciones de la ecuación de Klein-Gordon en ambos sistemas se llega a que los operadores de creación y destrucción van a cambiar.

Formulación en la que se muestra que el operador destrucción del primer espacio operando sobre el estado cero del primer espacio siempre da cero. En cambio este mismo operador en el tercer espacio operando sobre el estado cero del primer espacio da diferente de cero.

En presencia de un espacio-tiempo curvado, estos operadores deben volver a definirse dando como resultado de una combinación lineal de los operadores de creación y destrucción originales. Si el operador destrucción ha cambiado, nuestra definición del vacío también.

La relación entre los operadores iniciales y los finales se calculó a partir de las llamadas transformaciones de Bogoliubov y nos dará un método para describir la creación de las partículas.

Texto: “Transformaciones de Boboliubov” Aparece esta transformación para el caso del operador destrucción: b sub w (operador destrucción final) = a la integral dw (un número complejo conjugado por el operador destrucción inicial menos otro número complejo conjugado por el operador creación). Abajo hay una nota en con el siguiente texto “un número complejo tiene parte real y parte imaginaria” abajo aparece lo siguiente: u = x (parte real) + yi (parte imaginaria) con i será la raíz de menos uno. Su complejo conjugado será u* = x – yi. Es decir, el número con la parte imaginaria cambiada de signo.

La idea que podemos sacar de aquí es que un espacio-tiempo curvado genera partículas. Y un agujero negro es curvatura. Hawking utilizó este método para calcular la cantidad de partículas generadas por un agujero negro. Resultado que se da tanto si rota como si no.

Calculó qué cantidad de partículas llegarían a emitir, dando una emisión que se dará mientras este exista. Además, este resultado es independiente de los detalles del colapso, solo importa el AN resultante.

La emisión no se dará necesariamente en el horizonte de sucesos, tal y como nos podríamos imaginar, si no que se emite desde una región llamada “atmósfera cuántica” que tendrá un radio de varias veces el radio del horizonte de sucesos del agujero negro.

Lo divertido de este resultado es que la temperatura resultante de esta emisión coincide con la estimada por la termodinámica de los agujeros negros. Hawking dio una prueba de que aquello a lo que tanto se oponía anteriormente era correcto.

Como dato curioso, podemos obtener este mismo resultado si lo que tenemos es un observador acelerado. Este observador verá una generación de partículas idéntica al caso de la radiación de Hawking si su aceleración es igual a la gravedad superficial del agujero negro.

A esto se le conoce como efecto Unruh y es otro ejemplo de cómo un cambio de métrica da lugar a la generación de partículas.

Texto: “EFECTO UNRUH” Debajo aparece la temperatura producida por las partículas generadas por este efecto, siendo esta T = aceleración*constante de Planck dividida entre (2*pi*velocidad de la luz*constante de Boltzmann). Si la aceleración es a = velocidad de la luz elevada a cuatro dividida entre (4 por constante de gravitación universal y la masa del agujero negro), se recupera la misma temperatura que en el caso de un agujero negro sin rotación ni carga (agujero negro de Schwarzschild).

Aún nos queda un último punto. Si estamos viendo que los agujeros negros emiten partículas, eso implica que pierden masa ¿Pueden entonces llegar a desaparecer por este motivo?

La respuesta es afirmativa, estas partículas se generan a costa del agujero negro (de la curvatura del espacio-tiempo) lo que lleva a su evaporación. ¿Pero cuánto tiempo llevará este proceso y cómo sucederá?

Como ya hemos mencionado, la temperatura de un agujero negro es directamente proporcional a su gravedad superficial. Una cosa interesante de esto es que en cuanto más pequeño es un agujero negro mayor será su gravedad superficial.

Según cálculos del propio Hawking, cualquier agujero negro primordial con una masa menor de diez mil millones de toneladas ya se habrá evaporado. Como su gravedad superficial es mayor a la de un agujero negro mucho más masivo, su temperatura también es mayor.

La cantidad de partículas que emitirá crecerá en proporción a esto, lo que le llevará a ser cada vez más pequeño, lo que a su vez sigue aumentado la cantidad de partículas emitidas...Un círculo vicioso de manual. Y así hasta que se evapore completamente.

En el último instante de un agujero negro su emisión es tan intensa que es prácticamente una explosión. No demasiado intensa en términos astrofísicos, pero una explosión, al fin y al cabo.

No obstante, para un agujero negro de una masa estelar o incluso uno supermasivo el tiempo que tardará en evaporarse es mucho mayor que la edad actual del universo, muchos ordenes de magnitud por encima.

Volviendo a esa nave tuya desde la cual puedes divisar el agujero negro, y después de todo lo aprendido te preguntas si podrías medir esta radiación. La respuesta es que más bien no, y es la longitud de onda de estas partículas es tan grande como el propio agujero negro.

La consecuencia de esto es que te haría falta algo capaz de medir una longitud de onda así de grande. No obstante, aún podrías ver uno de los resultados más espectaculares y (casi) eternos de la naturaleza.

Bajo’s Substack

Discussion about this post